In a circuit where resistor A, inductor I, and capacitor C are connected in series, a phenomenon calledseries resonancemay occur. When an inductor is connected in series with active resistor A and capacitor, resonance phenomenon will be observed.

When there is series resonance in a circuit, the current and voltage are in phase, that is, the angle

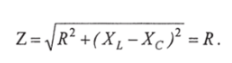
Obviously, if the conditions for series resonance occur, this equality will occur

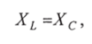
The reactance (X, X s) of the circuit is zero.

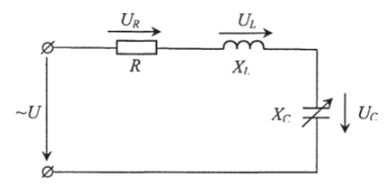
The frequencies of b, C, and the applied sine voltage represent X b and X c, respectively

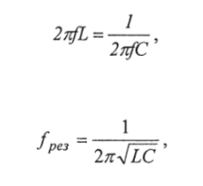
Therefore, at=X c, series resonance occurs in the circuit because the resonant frequency is equal to the frequency of the voltage supplied to the circuit.

According to Ohm's Law, the current in a circuit is:

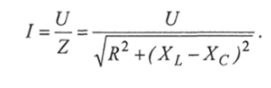
The analysis of this dependency shows that the current in the circuit during resonance (X b - X c=0) is equal to the voltage divided by the active resistance:

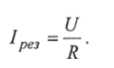
The current in the circuit reaches its maximum value because impedance 2 is very small (2=K).

The voltage on the active resistor duringseries resonanceis equal to the power supply voltage:

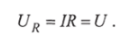
The figure shows the phase relationship between current and power supply voltage. The voltage across the active resistor is equal to the power supply voltage, and the voltage across the inductor and capacitor II is greater than the voltage

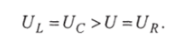
The phenomenon in which the voltage on the inductance and capacitance of a circuit exceeds the power supply voltage under certain conditions (XI=X C>I) is called series resonance.

Among them, the power factor of the circuit is equal to one:

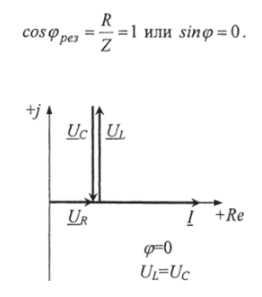
The active power of a circuit is equal to the total power:

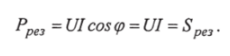
The reactive power of the circuit is zero:

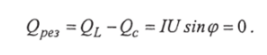
Due to stress resonance occurring under the condition X L=X C:

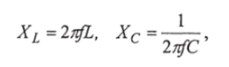
So resonance can be obtained by selecting the parameters (L, C) of the circuit for a given frequency (f=const) of the network, or by selecting the frequency of the network for a given parameter (L=const, C=const) of the circuit.

Therefore, in the resonant mode RL C, the circuit only consumes active energy from the network (with pure active characteristics) and does not consume reactive energy (Q=0). In this case, reactive energy periodically transfers from the electric field of the capacitor to the magnetic field of the inductor, and vice versa.